Understanding percentages can feel like deciphering a secret code, especially for those just beginning to explore its practical applications. Imagine a cashier giving you change, a student calculating exam scores, or a business evaluating growth; each scenario involves interpreting parts of a whole through the lens of percent. This article aims to provide a comprehensive, ground-level view of what 20 of 80 means within the broader context of percentage concepts, offering clarity for novices and even seasoned practitioners seeking a refresher. From fundamental principles to real-world examples, we'll journey through the essential techniques and considerations that make percentage calculations both intuitive and applicable across various domains.
The Concept of Percentages: A Foundation in Context

A percentage is essentially a way to express a ratio or a fraction in terms of 100, making it easier to compare parts of a whole. When you say “20 of 80,” you are referring to a specific part (20) relative to a total (80), which can be converted into a percentage to understand its significance in relation to the entire. This conversion is fundamental across disciplines—whether assessing market share, academic grades, or data distributions—because it offers a uniform, scalable measure of proportion. Mastering this concept involves understanding that percentages bridge the gap between parts and wholes, providing a meaningful context for evaluation and decision-making.
Practical daily application of percentages
For someone dealing with finances, estimation, or even health metrics, interpreting 20 of 80 through percentage calculations facilitates quick, informed evaluations. For example, calculating the percentage of a test score helps students gauge their performance, while consumers estimating discounts or taxes rely on similar mental math. This widespread utility underscores the importance of understanding percentages not just as abstract numbers but as practical tools embedded in daily life and professional routines.
| Relevant Category | Substantive Data |
|---|---|
| Basic Ratio Conversion | 20 ÷ 80 = 0.25 |
| Percentage Equivalent | 0.25 × 100 = 25% |
| Application Context | 20 out of 80 represents 25% of the total |

Step-by-step breakdown of calculating 20 of 80 as a percentage

To convert the ratio 20 of 80 into its percentage form, start with the basic ratio: 20 divided by 80. This yields 0.25, representing the proportion of the part relative to the whole. Multiplying this decimal by 100 translates it into a percentage, producing 25%. This process exemplifies a clear, replicable method for converting any part-whole ratio into a percentage, fostering analytical confidence across varying contexts.
Delving into division and multiplication techniques
Division acts as the gateway to understanding fractions of a whole—breaking down complex ratios into manageable figures. In this case, 20 ÷ 80 simplifies to 0.25, a decimal that encapsulates the ratio’s essence. Subsequent multiplication by 100 transforms this decimal into a more intuitive percentage form, 25%. This straightforward two-step process—divide then multiply—serves as a universal approach, adaptable for calculating discounts, statistical data, or performance metrics.
| Relevant Category | Substantive Data |
|---|---|
| Division Result | 20 ÷ 80 = 0.25 |
| Percentage Calculation | 0.25 × 100 = 25% |
Interpreting the result: What does 25% signify?
In essence, 25% indicates that the part (20) constitutes a quarter of the total (80). In educational contexts, if a student scores 20 points out of 80 on a test, they achieved 25%, providing a clear metric of their performance relative to the maximum possible score. Commercially, a 25% discount means a quarter off the original price, facilitating quick mental calculations during shopping or budget planning. The interpretive power of percentages lies in their ability to turn abstract ratios into intuitive, comparable figures that inform better decisions across life domains.
Beyond the number: implications and insights
Understanding what a percentage means in tangible terms can influence strategic choices. For instance, recognizing that 20 out of 80 is 25% helps businesses assess market penetration, or educators gauge the difficulty level of assessments. This clarity fosters more accurate evaluations, whether optimizing inventories, setting pricing strategies, or appraising progress toward goals. Percentages serve as a universal language—bridging data and real-world actions effectively.
| Related Metric | Explanation |
|---|---|
| Percent as Part of Real Data | With 25%, a quarter of the total is represented, guiding actionable insights |
| Impact on Decision-Making | Knowledge of exact percentages can influence strategic planning and resource allocation |
Advanced considerations and common pitfalls in percentage calculations
While the calculation 20 of 80 to 25% appears straightforward, everyday scenarios often introduce complexities such as varying denominators, partial data, or misinterpretations. For example, misapplying the percentage formula to non-whole numbers or inconsistent base figures can lead to errors. It’s also common to confuse the numerator and denominator or overlook the importance of units and context. Developing awareness of these pitfalls is crucial for maintaining accuracy, especially in professional settings like financial analysis or scientific research where precision is paramount.
Addressing ambiguity in real-world calculations
In many cases, data is incomplete or ambiguous. Ensuring clarity involves confirming the total figure when dealing with partial datasets or estimating proportions with confidence intervals. Furthermore, understanding the difference between percentage increase and percentage of a total avoids common misconceptions that can skew interpretations and decision-making processes.
| Potential Issue | Implication |
|---|---|
| Incorrect denominator | Misleading percentages that do not truly reflect the ratio |
| Confusing percentage increase with part-to-whole percentage | Misinterpretations of growth or decline |
Applying the learned calculation to broader contexts
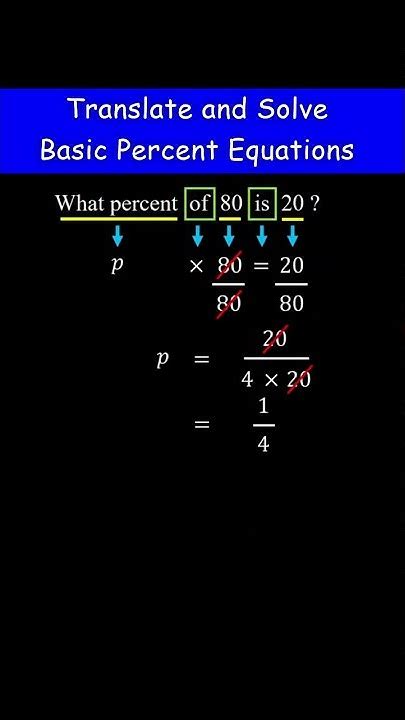
Once comfortable with the fundamental conversion of 20 of 80 into 25%, one can extend this approach across diverse areas. In finance, understanding proportions of investments; in health, calculating body fat percentages; or in project management, assessing task completion rates—all rely on similar calculation methods. Recognizing patterns and practicing with real data enhances efficiency, accuracy, and confidence in complex analytical tasks. Integrating this basic skill into daily routines cultivates a data-literate mindset that empowers strategic thinking and operational agility.
Real-world examples demonstrating broader applications
Consider a marketing analyst evaluating a campaign that reached 20,000 people out of a target audience of 80,000. Calculating that reach as a percentage (25%) helps assess campaign effectiveness. In inventory management, stocking 20 units out of an expected 80 indicates 25%, revealing stockout or supply chain issues. These examples illustrate that mastering basic percentage calculations unlocks insights pivotal for operational excellence.
| Application Area | Typical Data |
|---|---|
| Marketing Reach | 20,000 out of 80,000 = 25% |
| Inventory Management | 20 units out of 80 = 25% |
| Health Metrics | Body fat percentage calculations |
How do I convert a ratio like 20 of 80 into a percentage?
+Divide the part (20) by the whole (80) to get a decimal (0.25), then multiply by 100 to convert to a percentage (25%).
Can I use this method for any numbers?
+Yes, this division and multiplication approach works universally for converting any ratio into a percentage, regardless of the data’s context or scale.
What are common mistakes when calculating percentages?
+Mistakes include incorrect division, confusing numerator and denominator, or misinterpreting the context—such as mixing up percentage of increase with part-to-whole percentages.



