When dealing with rational functions, one of the key concepts to understand is the vertical asymptote. A vertical asymptote is a vertical line that a function approaches but never touches. In the context of rational functions, vertical asymptotes occur where the denominator of the function is equal to zero, causing the function to become undefined. Understanding vertical asymptote rules is crucial for graphing rational functions, analyzing their behavior, and solving problems in calculus and algebra.
Key Points
- The vertical asymptote of a rational function occurs at the value of x that makes the denominator equal to zero, provided that any common factors between the numerator and denominator have been canceled out.
- To find vertical asymptotes, factor the denominator and set each factor equal to zero to find the values of x.
- Holes in the graph occur where there are common factors between the numerator and denominator, which indicate points where the function is undefined but does not have a vertical asymptote.
- The presence of a vertical asymptote indicates that the function approaches positive or negative infinity as x approaches the asymptote from either side.
- Graphing rational functions involves understanding the behavior of the function near its vertical asymptotes, including whether the graph approaches the asymptote from the top or bottom and the direction of the function as it moves away from the asymptote.
Identifying Vertical Asymptotes

Identifying vertical asymptotes involves factoring the denominator of the rational function and setting each factor equal to zero. For example, consider the function f(x) = 1 / (x - 2). The denominator is already factored, so we set x - 2 = 0 to find the vertical asymptote at x = 2. This means that as x approaches 2 from the left or the right, the function f(x) approaches either positive or negative infinity.
Factors and Common Factors
When the denominator has multiple factors, each factor that is not canceled out by a corresponding factor in the numerator represents a potential vertical asymptote. For instance, consider f(x) = (x + 1) / (x - 2)(x + 3). Here, the potential vertical asymptotes are at x = 2 and x = -3, because these are the values that make the denominator zero. However, if there were a common factor between the numerator and the denominator, such as (x - 2), that factor would create a hole at x = 2 rather than a vertical asymptote, because the factor would cancel out, leaving no division by zero at that point.
| Function | Denominator Factors | Vertical Asymptotes |
|---|---|---|
| f(x) = 1 / x | x | x = 0 |
| f(x) = (x + 2) / (x - 1)(x + 3) | (x - 1), (x + 3) | x = 1, x = -3 |
| f(x) = x / (x^2 - 4) | (x + 2), (x - 2) | x = -2, x = 2 |
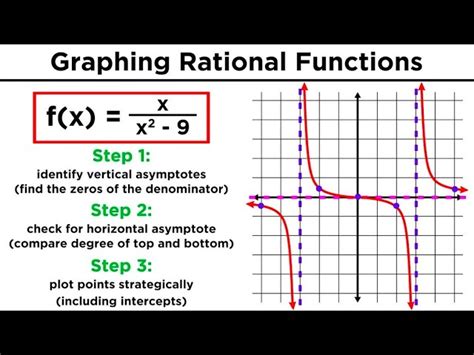
Graphing and Analyzing Behavior

When graphing rational functions, understanding the vertical asymptotes is crucial. The graph will approach the vertical asymptote but never cross it. The behavior of the function as it approaches the asymptote (from either side) can be determined by analyzing the sign of the function in the intervals surrounding the asymptote. For example, if f(x) = 1 / (x - 2), as x approaches 2 from the left (x < 2), f(x) becomes more negative (approaching negative infinity), and as x approaches 2 from the right (x > 2), f(x) becomes more positive (approaching positive infinity).
Sign Analysis
A sign analysis can help in understanding the behavior of the function around its vertical asymptotes. By testing a value of x in each interval separated by the vertical asymptotes, you can determine the sign of the function in that interval. This analysis is essential for sketching the graph of the rational function accurately and for understanding the function’s behavior in the vicinity of its vertical asymptotes.
In conclusion, vertical asymptotes are a critical aspect of rational functions, influencing the graph's shape and the function's behavior. By understanding the rules for identifying vertical asymptotes and analyzing the function's behavior around these points, you can gain deeper insights into the properties of rational functions and their applications in various mathematical and real-world contexts.
What is a vertical asymptote in a rational function?
+A vertical asymptote is a vertical line that a rational function approaches but never touches, occurring at values of x that make the denominator equal to zero.
How do you find the vertical asymptotes of a rational function?
+To find vertical asymptotes, factor the denominator of the rational function and set each factor equal to zero. The values of x that result are the locations of the vertical asymptotes, provided there are no common factors with the numerator that would create holes instead.
What is the difference between a vertical asymptote and a hole in a rational function?
+A vertical asymptote occurs where the denominator is zero and there are no common factors with the numerator, causing the function to approach infinity. A hole, on the other hand, occurs where there is a common factor between the numerator and the denominator, which cancels out, leaving a point where the function is undefined but does not approach infinity.
