Type 1 and Type 2 errors are fundamental concepts in statistical hypothesis testing, playing a crucial role in decision-making processes across various fields, including medicine, social sciences, and engineering. Understanding these errors is essential for interpreting test results accurately and making informed decisions. In this article, we will delve into the definitions, implications, and differentiation between Type 1 and Type 2 errors, as well as discuss strategies for minimizing their occurrence.
Key Points
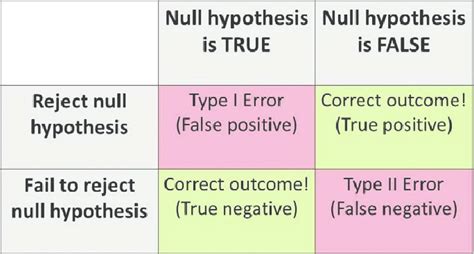
- Type 1 errors occur when a true null hypothesis is incorrectly rejected, often denoted as alpha (α) errors.
- Type 2 errors happen when a false null hypothesis is failed to be rejected, commonly referred to as beta (β) errors.
- The power of a test is its ability to correctly reject a false null hypothesis, directly related to Type 2 errors.
- Striking a balance between Type 1 and Type 2 errors is crucial, as decreasing one type of error often increases the other.
- Sample size, effect size, and the chosen significance level are critical factors in controlling both types of errors.
Understanding Type 1 Errors

A Type 1 error, also known as a false positive, occurs when a statistical test incorrectly rejects a true null hypothesis. This means that the test suggests there is an effect or relationship when, in fact, there is none. The probability of committing a Type 1 error is denoted by the Greek letter alpha (α) and is typically set at 0.05 in many fields, although this value can be adjusted based on the study’s requirements and the desired level of confidence.
Implications of Type 1 Errors
The implications of Type 1 errors can be significant, leading to unnecessary interventions, wasted resources, and, in some cases, harm to individuals or communities. For instance, in medical research, a Type 1 error could lead to the adoption of ineffective treatments or the unnecessary use of harmful drugs. In social sciences, a false positive could result in misguided policies or interventions that do not address the actual issues at hand.
Understanding Type 2 Errors
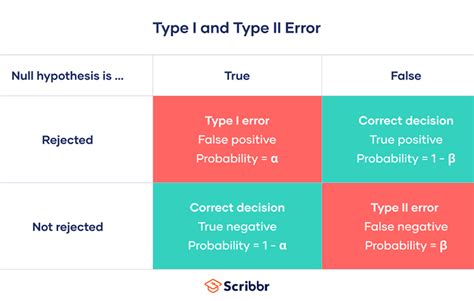
A Type 2 error, or false negative, occurs when a statistical test fails to reject a false null hypothesis. This means that the test fails to detect an effect or relationship that is actually present. The probability of committing a Type 2 error is denoted by the Greek letter beta (β), and the power of a test (1 - β) is its ability to correctly reject a false null hypothesis.
Implications of Type 2 Errors
Type 2 errors can also have substantial implications, particularly in contexts where failing to detect a real effect can lead to missed opportunities for improvement or intervention. In clinical trials, for example, a Type 2 error could result in a beneficial treatment being overlooked. In environmental science, failing to detect harmful effects of pollutants could lead to inadequate regulations and continued environmental degradation.
Minimizing Type 1 and Type 2 Errors
Minimizing both Type 1 and Type 2 errors requires careful planning and execution of statistical tests. Increasing the sample size can reduce both types of errors by providing more precise estimates of the population parameters. The effect size, or the magnitude of the effect being studied, also plays a critical role, as larger effects are easier to detect. Additionally, choosing an appropriate significance level (α) involves balancing the risk of Type 1 errors against the risk of Type 2 errors.
| Error Type | Description | Probability |
|---|---|---|
| Type 1 Error | Rejecting a true null hypothesis | α (Alpha) |
| Type 2 Error | Failing to reject a false null hypothesis | β (Beta) |

Strategic Considerations
In practice, minimizing Type 1 and Type 2 errors involves strategic considerations, including the design of experiments, the selection of appropriate statistical tests, and the interpretation of results within the context of the research question or practical problem. Technological advancements and computational power have also enabled the use of more sophisticated statistical techniques, such as Bayesian analysis, which can provide additional insights and flexibility in hypothesis testing.
Bayesian Approach
The Bayesian approach to hypothesis testing offers an alternative to traditional frequentist methods, allowing for the incorporation of prior knowledge and the updating of beliefs based on new data. This approach can be particularly useful in situations where there is significant prior information or when the consequences of Type 1 and Type 2 errors are asymmetrical.
What is the primary difference between Type 1 and Type 2 errors?
+Type 1 errors involve rejecting a true null hypothesis, while Type 2 errors involve failing to reject a false null hypothesis.
How can the risk of Type 1 and Type 2 errors be minimized?
+Increasing the sample size, carefully selecting the significance level, and considering the effect size can help minimize both types of errors.
What role does the Bayesian approach play in hypothesis testing?
+The Bayesian approach allows for the incorporation of prior knowledge and the updating of beliefs based on new data, providing an alternative to traditional frequentist methods.
In conclusion, understanding and managing Type 1 and Type 2 errors is crucial for the validity and reliability of statistical inferences. By recognizing the implications of these errors and employing strategies to minimize their occurrence, researchers and practitioners can enhance the quality of decision-making across various disciplines. The delicate balance between these two types of errors underscores the importance of careful study design, appropriate statistical analysis, and thoughtful interpretation of results.