Understanding how to graph derivatives of functions is akin to learning to read the DNA of a complex organism: it reveals the underlying structure and behavior, transforming a raw data set into meaningful insights. Just as a biologist deciphers genetic codes to understand an organism’s traits, a mathematician or student must interpret the original graph and its derivative to grasp the rate at which the function changes. This guide offers a comprehensive, step-by-step approach, blending foundational principles with practical techniques, to empower learners and professionals alike in mastering the art of graphing derivatives. By framing the process through an intuitive analogy, each stage becomes part of a cohesive narrative that simplifies complexity and fosters confidence.
The Foundation: Visualizing and Understanding the Original Graph
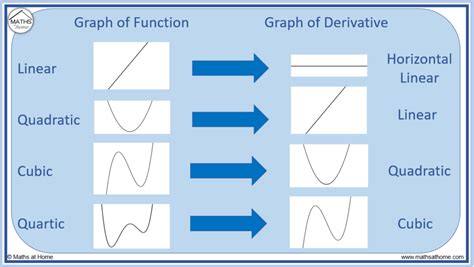
Before venturing into the derivative’s graph, it’s essential to develop a clear mental image of the original function—its shape, key points, and overall behavior. Think of this as preparing the terrain before charting a new map. Recognizing the peaks, valleys, inflection points, and asymptotes on the original graph provides vital clues about the corresponding derivative. For example, where the original graph reaches a maximum or minimum, the derivative crosses zero; at points of inflection, the derivative’s slope changes characteristically. Building a detailed mental model ensures that each derivative point is rooted in the context of the original function’s geometry.
Step 1: Identify Critical Points and Behavior of the Original Graph

Critical points—where the slope of the original graph is zero—serve as landmarks on the derivative plot. To locate these, focus on the derivative’s relationship to the original: where dy/dx equals zero, the graph of the original reaches local maxima or minima. Examining the original graph’s increasing or decreasing intervals aids in predicting the positive or negative signs of the derivative. For instance, if the original graph rises from left to right, its derivative is positive; if it falls, the derivative is negative.
| Relevant Category | Substantive Data |
|---|---|
| Critical Point | Where dy/dx=0; corresponds to local maxima and minima |

Step 2: Find Inflection Points and Curvature Changes
Inflection points on the original graph—where concavity shifts—are mirrored by zero crossings in the second derivative, d²y/dx². Tracking the concavity helps clarify where the slope of the derivative reaches its own maxima or minima. When the original graph transitions from concave up to concave down, the first derivative has a local extremum—this is a crucial element in sketching the derivative’s shape. Noting the regions of increasing or decreasing concavity informs the curvature of the derivative graph itself.
| Relevant Category | Substantive Data |
|---|---|
| Inflection Points | Where the second derivative equals zero; indicates curvature change |
Step 3: Using Derivative Rules for Graph Sketching
To construct the derivative graph accurately, applying fundamental differentiation rules—power rule, product rule, quotient rule, chain rule—is necessary. These rules translate the algebraic behavior into the visual behavior of the derivative. For polynomial functions, the process resembles calculating the slope of each segment explicitly; for more complex functions like exponentials or trigonometry, understanding their derivatives’ properties helps anticipate the shape of the graph. Recognizing where the derivative is undefined, such as at discontinuities or cusps, is vital for a precise plot.
Visualizing Derivative Sign and Behavior
Attentively examining the derivative’s sign on a plot provides immediate insights into the original: positive derivative indicates increasing functions, negative signals decreasing ones. The magnitude of the derivative influences the steepness of the tangent lines at various points. Graphing systematically at critical points, inflection points, and key intervals yields a comprehensive derivative plot.
Refining with Technology and Analytical Tools
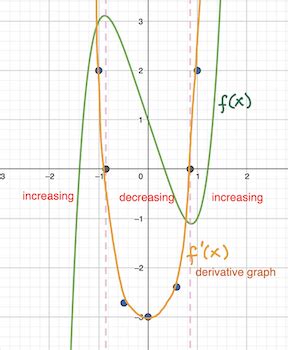
Modern calculus heavily relies on computational tools like graphing calculators, Desmos, or Wolfram Alpha—these function as digital cartographers providing detailed plots of both functions and derivatives. They serve as an experimental sandbox, where adjusting parameters reveals the immediate reaction of the derivative graph, solidifying intuition. Furthermore, these tools assist in verifying hand-drawn sketches, especially for intricate functions where analytical calculation becomes cumbersome.
Practical Applications and Advanced Techniques
The process of graphing derivatives isn’t just academic—its applications span physics, engineering, economics, and beyond. Engineers analyze stress-strain charts to determine rates of change; economists examine cost functions to optimize revenue; physicists interpret acceleration graphs from velocity data. Advanced techniques involve using derivative tests—like the First and Second Derivative Tests—to confirm local extrema and concavity, ensuring a robust understanding that extends beyond mere sketching.
Handling Complicated Functions
Functions with multiple critical points, asymptotes, or oscillations demand a layered approach, akin to mapping rugged terrain with numerous peaks and valleys. Segmenting the domain into manageable parts and applying derivative rules and sign analysis in each region improves accuracy and clarity. Symbolic computation software can handle such complexity, but developing the skill to interpret and verify the plots remains quintessential.
| Relevant Category | Substantive Data |
|---|---|
| Complex Function Handling | Partitioning domain; applying piecewise analysis; using computational tools |
Common Pitfalls and How to Avoid Them
Misinterpreting critical points, neglecting points of discontinuity, or confusing the zero crossings of derivatives with inflection points often lead to inaccuracies. Like navigating a maze with dead ends, attention to detail—marking where derivatives are undefined and confirming sign changes—prevents errors. Regular cross-referencing with the original graph ensures that the derivative’s shape aligns perfectly with the function’s behavior, avoiding common oversight.
Summary: Building Your Derivative Mapping Skillset
Mastering the graphing of derivatives is about cultivating a keen eye for detail and understanding the symbiotic relationship between a function and its rate of change. It transforms abstract calculus rules into tangible visualizations—akin to a cartographer meticulously charting terrain. By systematically analyzing critical points, inflection points, and applying derivative rules, an individual develops a powerful tool for scientific and analytical exploration. As with any complex skill, practice and the utilization of technological aids accelerate mastery, turning the seemingly intricate art of graphing derivatives into an intuitive, rewarding process.
Key Points
- Understanding the original graph is essential for accurate derivative plotting, acting as the terrain on which the derivative map is built.
- Locating critical points and inflection points provides landmarks that guide the shape of the derivative graph.
- Applying differentiation rules systematically transforms the algebraic form into visual change, plotting the slope at each region.
- Technology integration enhances precision and visual clarity, especially for complex functions.
- Attention to detail in recognizing discontinuities and sign changes is vital to avoid common errors.
- Overall mastery converts calculus from rote computation into insightful visualization, empowering more effective analysis across disciplines.
What is the primary principle behind graphing derivatives?
+The primary principle is that the derivative graph reflects the slope of the original function at each point, providing the rate of change which helps visualize increasing/decreasing trends and extremal points.
How do critical points on the original graph relate to the derivative?
+Critical points occur where the original graph has zero slope, meaning the derivative crosses zero; these points often correspond to local maxima or minima on the original function.
Can technology reliably replace manual graphing?
+While software tools significantly enhance accuracy and efficiency, understanding the underlying principles remains crucial. Manual sketching fosters intuition that technology alone cannot substitute.
How do inflection points on the original graph influence its derivative?
+Inflection points, where the curvature changes, are reflected by zero crossings or extrema in the first derivative; they indicate significant shifts in the rate of change.
What are common mistakes to avoid when graphing derivatives?
+Common errors include misidentifying critical points, overlooking discontinuities, and confusing zero crossings of derivatives with inflection points, all of which distort the true behavior of the function.